Перцептронът - основа на невронните мрежи

Въведение

Работата на Франк Розенблат (Frank Rosenblatt) постави основите на съвременните невронни мрежи. Той създаде принципи, които остават актуални и до днес, и положи фундамента за по-нататъшни изследвания в областта на машинното обучение. В тази статия ще представя основните идеи, които той предложи, и ще опитам да проведа паралели със съвременните невронни мрежи. Също така ще покажа как да реализираме перцептрон на Python с използването на библиотеката NumPy.

Какво е неврон?

Нашият мозък се състои от милиарди клетки, наречени неврони. Невронът е основната единица на нервната система, която отговаря за предаването и обработката на информацията.

Неврон или нервна клетка (от др.-гр. νεῦρον “влакно; нерв”) — тясно специализирана клетка. Невронът е електрически възбудима клетка, предназначена за приемане извън, обработване, съхранение, предаване и извеждане извън информацията с помощта на електрически и химически сигнали. (Wikipedia)

Всеки неврон получава сигнали от други неврони и ги предава по-нататък. Невроните са свързани помежду си чрез синапси, които им позволяват да обменят информация.

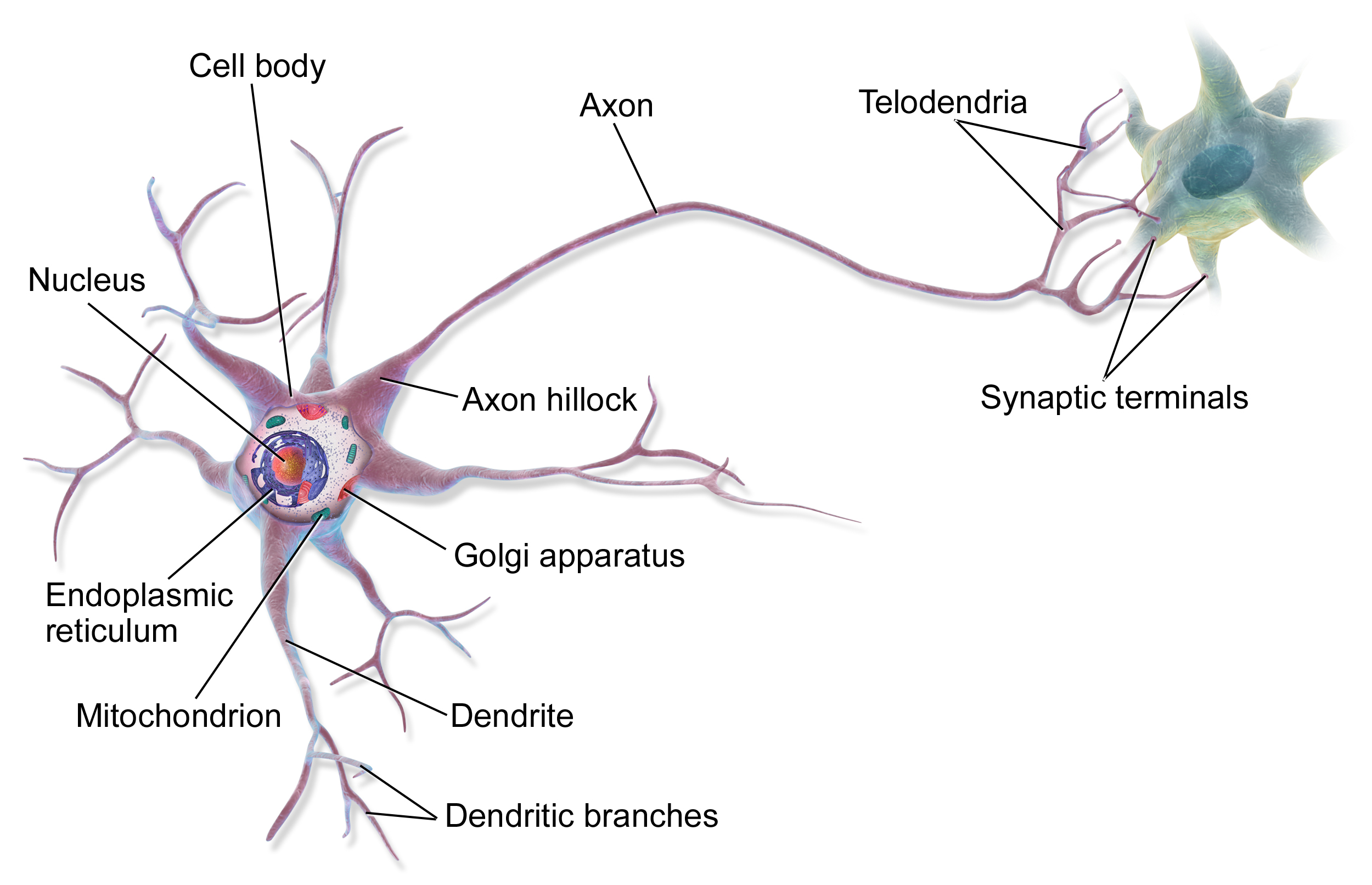
Neuron — Схема на неврон (by BruceBlaus взето от Wikipedia)

Да обърнем внимание на дендритите и аксона. Дендритите приемат сигнали от други неврони, а аксонът предава сигнали по-нататък. Всеки неврон може да има множество дендрити и един аксон (в повечето случаи). Сигналите, които невронът получава от други неврони, могат да бъдат както възбуждащи, така и потискащи. Възбуждащите сигнали увеличават вероятността невронът да “сработи” (т.е. да предаде сигнал нататък), а потискащите — намаляват тази вероятност.

Така през 1957 г. Франк Розенблат предложи модел на неврон, който нарече перцептрон.

Какво е перцептрон?

Перцептронът е най-простият модел на невронна мрежа, която се състои от един неврон. Той приема няколко входни сигнала, обработва ги и дава един изходен сигнал.

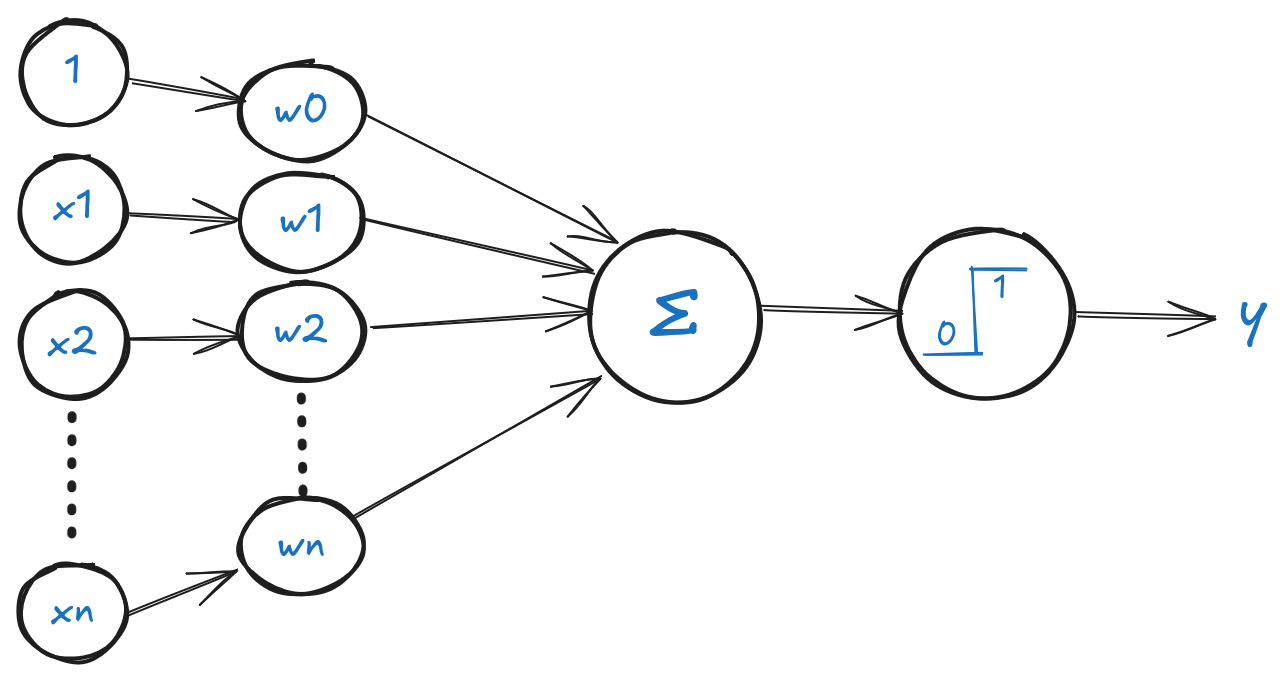
В своя модел, Розенблат използва няколко входа, всеки от които има свое тегло. Теглото е число, което показва колко важен е този вход за неврона. Колкото по-голямо е теглото, толкова по-голямо е влиянието на този вход върху изхода на неврона.
Входовете и теглата се умножават, и след това всички произведения се сумират. Ако сумата е по-голяма от прага, то невронът “сработва” и дава сигнал 1, иначе — 0. Прагът е число, което показва колко силен трябва да бъде сигналът, за да “сработи” невронът. Прагът може да се счита за тегло, което се умножава по 1 (входът винаги е равен на 1).

В съвременните невронни мрежи прагът обикновено се заменя с функция на активация, която позволява на неврона да “сработва” при определени условия. Функцията на активация може да бъде линейна или нелинейна. При линейна функция на активация изходът на неврона е пропорционален на входа, а при нелинейна — изходът зависи от входа по сложна формула.

Нека запишем формулата на перцептрона:

Ако на входа имаме вектор $x = (x_1, x_2, \ldots, x_n)$, а на изхода — число $y$. Тогава формулата на перцептрона изглежда така:

Сума на всички входове, умножени по теглата:

$$ z^{(i)} = \theta_0+\theta_1x_1^{(i)} + \theta_2x_2^{(i)} + ... + \theta_nx_n^{(i)} = \theta^Tx^{(i)} \tag1$$

където i - номер на примера, $\theta$ - вектор на теглата, $x^{(i)}$ - вектор на входовете.

Тогава функцията на активация (стъпкова функция):

$$ h(z)= \left\{ \begin{array}{rcr} 1 & z \geq 0 \\ 0 & в\: противен\: случай \\ \end{array} \right. \tag2 $$

Нека напишем код, който реализира перцептрона. Ще използваме библиотеката NumPy за работа с масиви и матрици. Също така ще използваме библиотеката Matplotlib за визуализация на данните.

import numpy as np
class Perceptron:
    def __init__(self):
        pass

    def net_input(self,X):
        return  np.dot(X, self.theta[1:]) + self.theta[0] # z

    def predict(self,X):
        return  np.where(self.net_input(X) >= 0.0, 1, 0) # h(z)

Вероятно сте забелязали в кода, че сме добавили единица към теглата. Това се прави, за да се вземе предвид прагът. Можем да считаме, че имаме допълнителен вход, който винаги е равен на 1. Този вход се умножава по тегло, което е равно на прага. По този начин можем да считаме, че прагът е тегло, което се умножава по 1.
Също така, първоначалните тегла не са ни известни, затова ги инициализираме с нули. И пред нас стои задачата да намерим такива тегла, които ще позволят на перцептрона правилно да класифицира данните.

Как да обучим перцептрона?

Преди да обучим перцептрона, нека определим какво е обучение. Обучението е процес, при който намираме такива тегла, които ще позволят на перцептрона правилно да класифицира данните. Т.е. имаме входни данни x₁…xₙ и изходни данни y (0 или 1), и искаме да намерим такива тегла $\theta$, които ще позволят на перцептрона правилно да класифицира данните.

За тази цел трябва да определим функция на загубата. Функцията на загубата е функция, която показва колко добре перцептронът класифицира данните. Колкото по-малка е стойността на функцията на загубата, толкова по-добре перцептронът класифицира данните (толкова по-малки са загубите - оттук и името).

$$ error^{(i)} = \frac12(h(z^{(i)}) - y^{(i)})^2 \tag3$$

Нека разберем защо в тази формула имаме квадрат. Ако бихме използвали просто разликата, то при обучение перцептронът би могъл да се “обърква” в знаците.

Тогава общата функция на загуба ще бъде равна на:

$$ L(\theta) = \frac{1}{2m} \sum_{i=1}^{m} (h(z^{(i)}) - y^{(i)})^2 \tag4 $$

Делим резултата на m, за да получим средната стойност на загубите. m е броят на примерите в обучаващата извадка.

Ако предсказваме 1, а в действителност е 0, то грешката ще бъде равна на (1-0) = 1, а ако е обратното, то грешката ще бъде равна на (0-1) = -1. Ако бихме използвали просто разлика, то в първия случай грешката би била положителна, а във втория — отрицателна. И при сумиране грешките биха се взаимно унищожавали. Ако вземем квадрат, то в двата случая грешката ще бъде положителна. По този начин можем да считаме, че грешката е разстоянието от предсказанието до действителната стойност. Колкото по-малко е това разстояние, толкова по-добре перцептронът класифицира данните.
Тъй като данните са фиксирани, можем да ги считаме за константи. Тогава функцията на загубата ще зависи само от теглата $\theta$. Т.е. можем да считаме, че функцията на загубата е функция от теглата.

Тъй като нашата функция на загубата е квадратична, то нейната производна ще бъде линейна и ще е равна на 0 в точката на минимума. За опростяване на изчислението на производната, умножаваме функцията на загубата по 1/2 (това няма да повлияе на минимума, тъй като 1/2 е просто константа). Тогава производната за пример i ще бъде равна на:

$$ \frac{\partial{\frac12(\theta_0+\theta_1x_1^{(i)} + \theta_2x_2^{(i)} + ... + \theta_nx_n^{(i)} - y^{(i)} )^2}}{\partial{\theta_j}} = (h(z^{(i)}) - y^{(i)})x_j^{(i)} $$

и общата производна по правилото за сумата ще бъде равна на:

$$ \frac{\partial{L(\theta)}}{\partial{\theta_j}} = \frac{1}{m} \sum_{i=1}^{m} (h(z^{(i)}) - y^{(i)})x_j^{(i)} \tag5 $$

за j = 0, 1, …, n

За да решим задачата аналитично, би трябвало да приравним всяка частна производна на нула и да решим уравнението. Но това по правило е невъзможно да се направи. Ако имаме 100 примера по 100 признака във всеки (m = 100 и x₁…x₁₀₀), би трябвало да решим система от 100 уравнения със 100 неизвестни. Затова ще използваме числени методи за намиране на минимума на функцията на загубата. Един от най-простите и популярни методи е методът на градиентното спускане.

Градиентно спускане

Градиентното спускане е итеративен метод, който позволява да се намери минимум на функцията.

Идеята на този метод е в това, че ако променим теглото $\theta_j$ с малка стойност, то функцията на загубата (3) ще се промени приблизително с:

$$ \Delta{error} =(h(z^{(i)}) - y^{(i)})x_j^{(i)}\Delta{\theta_j} $$

Така, за да намалим грешката, трябва да променим теглото $\theta_j$ в посока, противоположна на производната (тъй като производната показва посоката, в която функцията расте). Т.е. трябва да намалим теглото, ако производната е положителна, и да увеличим теглото, ако производната е отрицателна. Можем да запишем това във вид на формула:

$$ \Delta{\theta_j} = \alpha = learningrate(стъпка\: на\: обучение) $$$$ \theta_j = \theta_j - \alpha(h(z^{(i)}) - y^{(i)}) x_j^{(i)} \tag6 $$

Стъпката на обучение не трябва да бъде твърде голяма, иначе можем да “прескочим” минимума и да започнем да се движим в друга посока. Ако стъпката на обучение е твърде малка, то процесът на обучение ще бъде твърде дълъг. Затова трябва да я подбираме експериментално.

Реализация

Нека сами напишем функция, която ще обучава перцептрона. Но първо да се определим с данните.

Един от най-популярните набори от данни за обучение на перцептрон е наборът от данни за ириси (Iris dataset). Той се състои от 150 примера, всеки от които има 4 признака (дължина и ширина на чашелистчето и венчелистчето) и 3 класа (видове ириси). Ние ще използваме само два класа (Setosa и Versicolor), за да опростим задачата (Wikipedia).

Нека инсталираме необходимите библиотеки и заредим данните:

pip install numpy matplotlib pandas

Сега да стартираме Jupyter Notebook и да заредим данните:

import pandas as pd

df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data',
                 header=None)
df.tail()

Резултат:

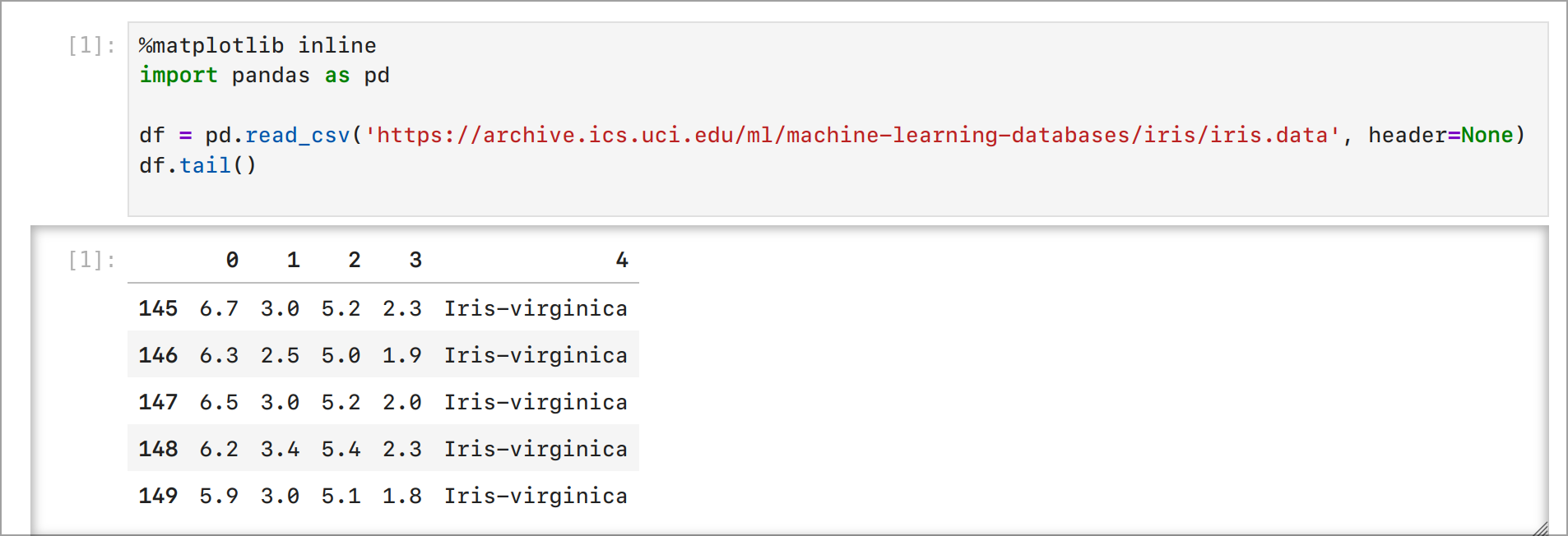
Нека визуализираме данните:

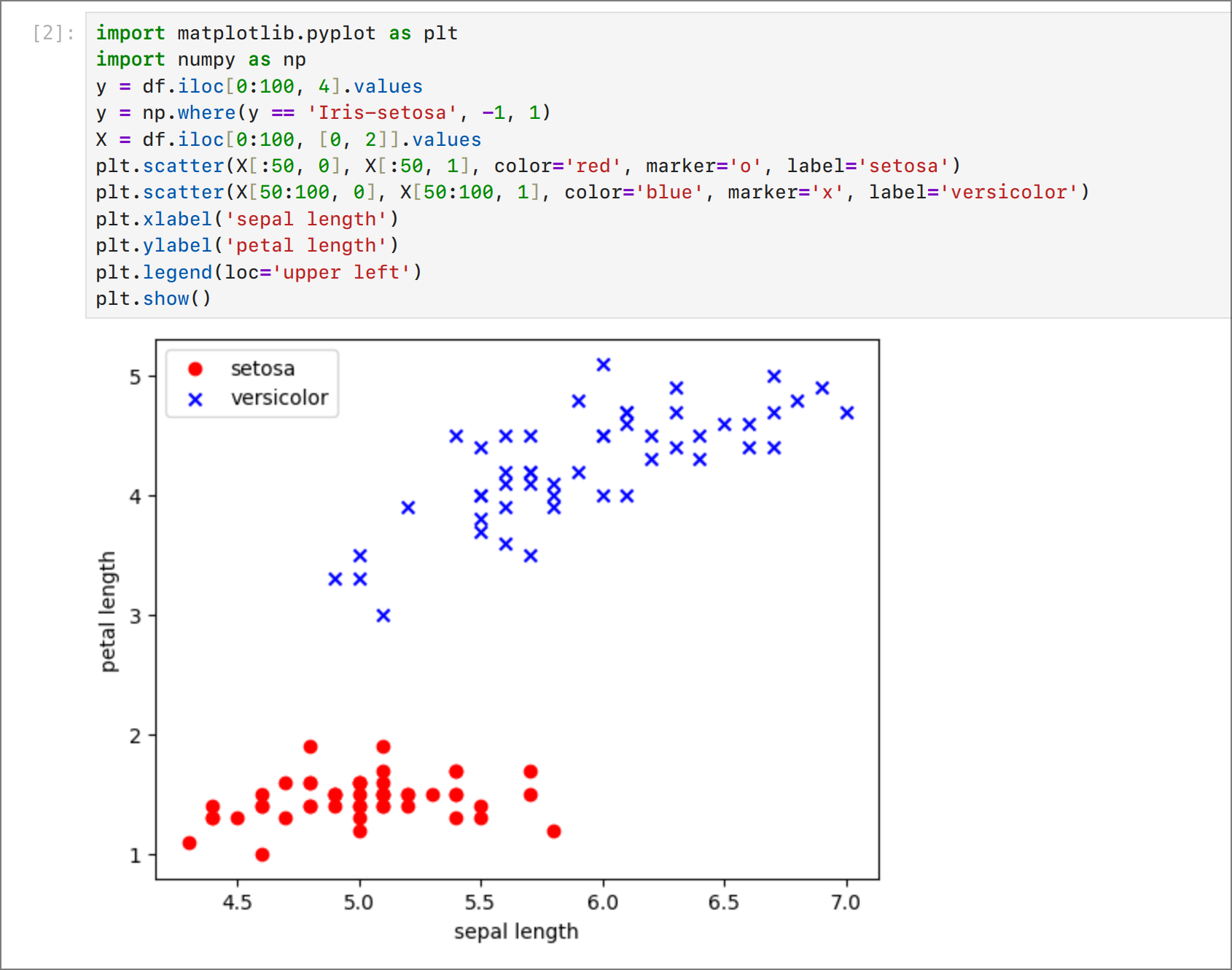
Можем да забележим, че данните са линейно разделими. Т.е. можем да прокараме права линия, която ще раздели данните на два класа. Това означава, че можем да използваме перцептрон за решаване на тази задача. Ако данните не бяха линейно разделими, то би трябвало да използваме по-сложни модели (например, многослойни невронни мрежи).

Нека обновим кода, така че да включва обучение на перцептрона (метод fit) и масив с грешки за проследяване на процеса на обучение:

import numpy as np
class Perceptron:
    def __init__(self,alpha=0.01, n_iter=10):
        self.alpha = alpha
        self.n_iter = n_iter
        self.wrong_classifications = []

    def fit(self, X, y):
        self.theta = np.zeros(X.shape[1] + 1) # тегла
        for _ in range(self.n_iter):
            wrong_classification = 0
            for xi, target in zip(X, y):
                update = self.alpha * (target - self.predict(xi))
                self.theta[1:] += update * xi
                self.theta[0] += update
                wrong_classification += int(update != 0.0)
            self.wrong_classifications.append(wrong_classification)
        return  self

    def net_input(self,X):
        return  np.dot(X, self.theta[1:]) + self.theta[0] # z

    def predict(self,X):
        return  np.where(self.net_input(X) >= 0.0, 1, 0) # h(z)

Сега нека извикаме метода fit и му предадем данните:

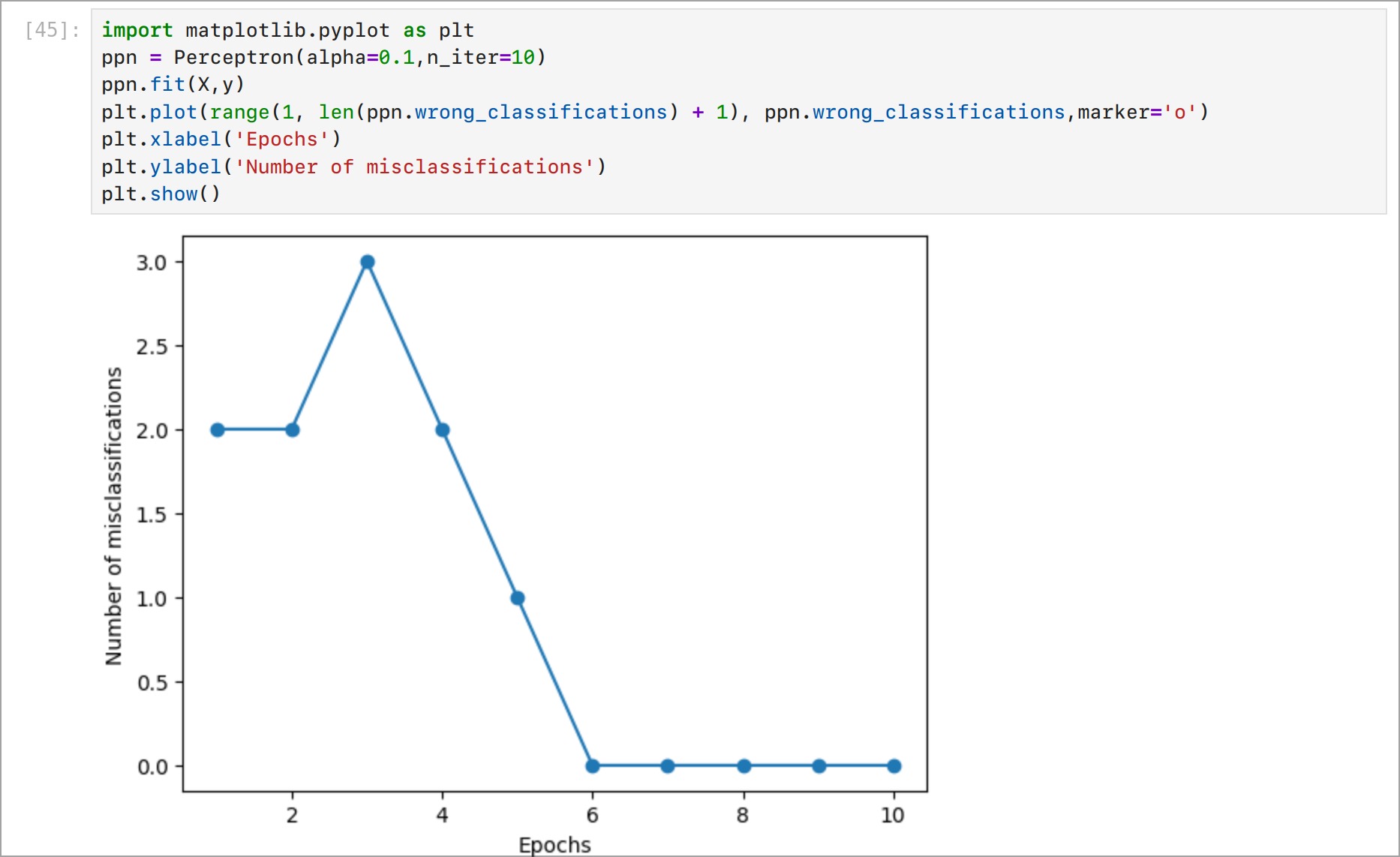
Както виждате, след 6 стъпки перцептронът се научи да класифицира данните. Сега нека погледнем границата на вземане на решение. Можем да визуализираме границата на вземане на решение, като използваме библиотеката Matplotlib.

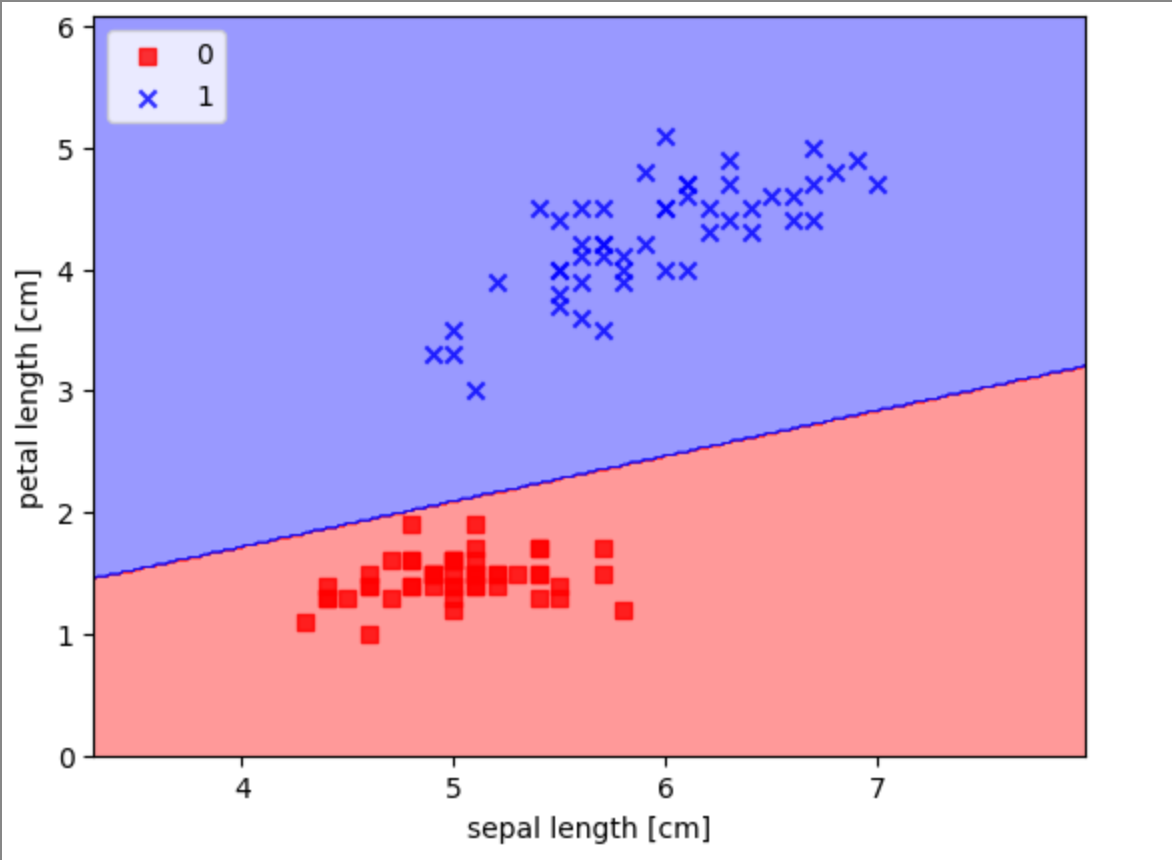
Decision boundary — Граница на вземане на решение

Заключение

В тази статия разгледахме перцептрон — най-простия модел на невронна мрежа. Разбрахме как работи и как да го обучим. Също така разгледахме метода на градиентното спускане, който позволява да се намери минимум на функцията на загубата. Надявам се, че тази статия ви беше полезна и ви помогна по-добре да разберете как работят невронните мрежи.

Перцептронът - основа на невронните мрежи.