Няколко думи за вероятността
Теорията на вероятностите е в основата на машинното обучение. Тя предоставя математически апарат за работа с несигурност и шум в данните — нещо неизбежно в реалния свят. Вероятностите изразяват степента на увереност в предсказанията, а много от моделите — като логистичната регресия, наивния баесов класификатор и дори невронните мрежи — се обучават чрез оптимизиране на функции, свързани с вероятности, като логаритъм на правдоподобието или крос-ентропия.
Байесовите методи позволяват включване на предварителни знания чрез априорни разпределения, а вероятностните оценки помагат при сравняване и избиране на модели. С други думи, теорията на вероятностите е езикът, чрез който формулираме, обучаваме и интерпретираме машинни модели.
В тази статия ще разгледаме основите на теорията на вероятностите, условната вероятност и теоремата на Бейс. Ще се опитам да обясня всичко по възможно най-простия начин, без сложни формули и термини (освен ако не е абсолютно необходимо). Статията е предназначена за начинаещи.
Вероятностно пространство, събития и вероятности
Множество
Нека започнем с определението на множество. Множеството е колекция от обекти, които могат да бъдат всичко: числа, хора, автомобили и т.н.
Множеството може да бъде крайно или безкрайно. Например, множеството на всички естествени числа (от 1 до безкрайност) е безкрайно, а множеството на всички хора на Земята е крайно.
Математически множеството се обозначава с фигурни скоби. Например, множеството на всички естествени числа от 1 до 10:
$$ \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\} $$Множеството може да бъде празно: \(\emptyset\) или \(\{\}\). Празното множество не съдържа нито един елемент.
Пример:
Множество на всички естествени числа:
$$ \mathbb{N} = \{1, 2, 3, 4, 5, \ldots\} $$Множество на всички цели числа:
$$ \mathbb{Z} = \{\ldots, -3, -2, -1, 0, 1, 2, 3, \ldots\} $$Множество на всички реални числа:
$$ \mathbb{R} = \{x \mid x \text{ е реално число}\} $$Подмножество
Ако множеството B е част от множеството A, то B е подмножество на A.
Например, ако \(A = \{1,2,3\}\), то възможните подмножества са: \(\emptyset\), \(\{1\}\), \(\{2\}\), \(\{3\}\), \(\{1,2\}\), \(\{1,3\}\), \(\{2,3\}\), \(\{1,2,3\}\).
Обозначава се като \(B \subseteq A\). Ако B не е подмножество на A, пишем \(B \nsubseteq A\).
Вероятностно пространство (Sample Space)
Вероятностното пространство е множеството на всички възможни изходи от експеримента.
Например, при хвърляне на зар вероятностното пространство е:
$$ S = \{1, 2, 3, 4, 5, 6\} $$При хвърляне на монета:
$$ S = \{\text{ези}, \text{тура}\} $$Ако хвърляме зара два пъти:
$$ S = \{ (1,1), (1,2), \ldots, (6,5), (6,6) \} $$Вероятностното пространство винаги зависи от конкретния експеримент, който провеждаме.
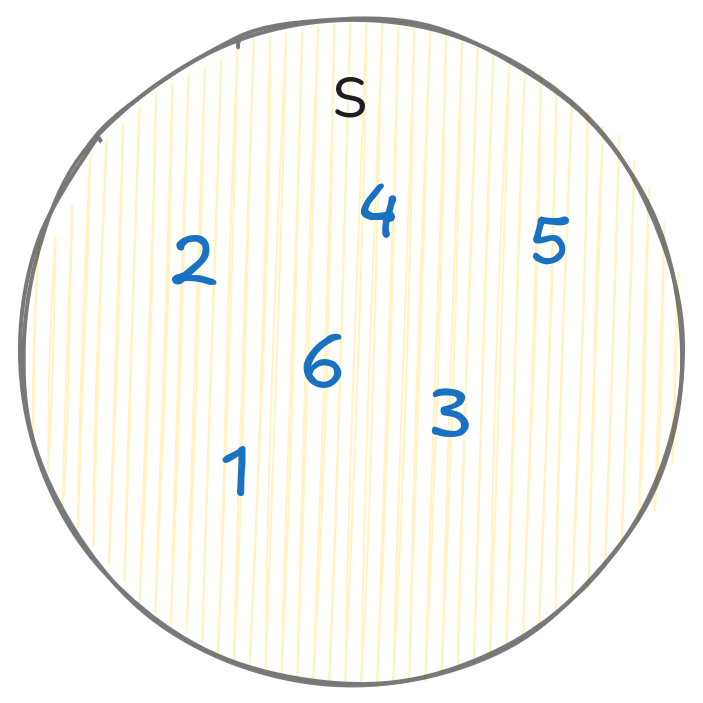
Пример за вероятностно пространство при хвърляне на зар:
Събитие
Всяко подмножество на вероятностното пространство се нарича събитие (ще го означим като E).
Например, при хвърляне на зар събитието “падна се четно число”:
$$ E = \{2, 4, 6\} $$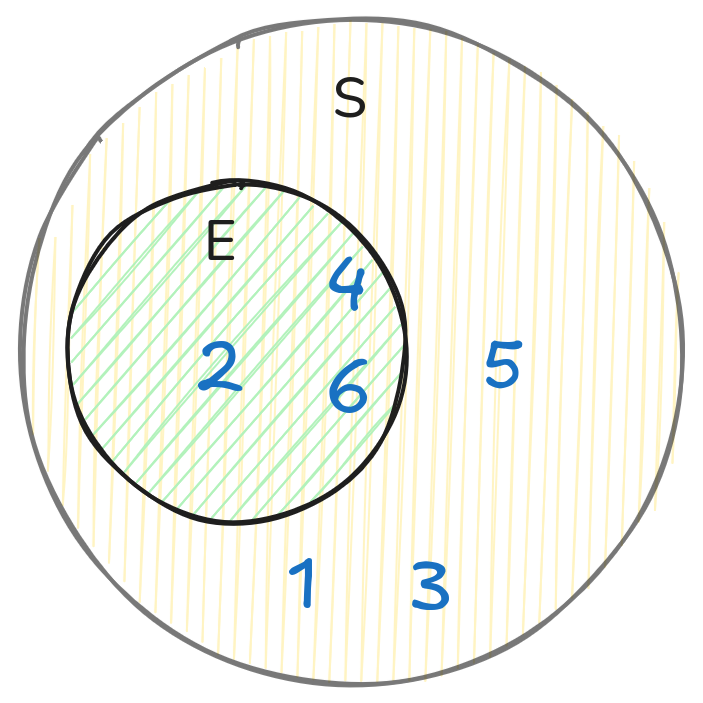
Да запомним: събитието \(E\) е подмножество на вероятностното пространство \(S\), т.е. \(E \subseteq S\).
E може да бъде празно (например, събитието “падна се число по-голямо от 6” при хвърляне на зар).
Вероятност
Вероятността е мярка за това колко е вероятно дадено събитие да се случи. Вероятността на събитието E се обозначава с \(P(E)\).
Интуитивно, вероятността на събитието E е отношението на броя на благоприятните изходи към общия брой изходи в вероятностното пространство (т.е. броя на елементите в E към броя на елементите в S):
$$ P(E) = \frac{|E|}{|S|} \tag{1} $$където \(|E|\) е броят на елементите в E.
Пример:
За примера със зара вероятността да се падне четно число:
$$ P(E) = \frac{3}{6} = \frac{1}{2} $$Тъй като \(|E| \leq |S|\), вероятността на събитието E винаги е в интервала от 0 до 1.
- При вероятност 0 събитието никога няма да се случи.
- При вероятност 1 събитието винаги ще се случи.
Важно: Да изчисляваме вероятността по такъв начин, чрез броене на благоприятните изходи, можем само ако всички изходи са равновероятни. Този подход се нарича класически.
Но ако, например, нашият зар е неравновероятен (с изместен център на тежестта), то вероятността да се падне 1, например, вече няма да бъде 1/6.
Ако поне един от изходите е по-вероятен, такъв метод престава да отразява реалната вероятност и трябва да използваме действителните честоти. Така, ако хвърляме зар 100 пъти и 20 пъти се пада 1, то вероятността да се падне 1 ще бъде 20/100 = 0.2.
В такава ситуация вероятността на ВСЯКО ОТДЕЛНО събитие може да се изчисли чрез честотния подход:
$$ P(x) = \frac{n(x)}{N} $$където \(n(x)\) е броят пъти, когато се е случило събитието x, а \(N\) е общият брой изпитания.
За нашия пример със зара и събитието “падна се четно число”:
$$ P(E) = \frac{n(E)}{N} = \frac{3}{6} = \frac{1}{2} $$където \(n(E)\) е броят пъти, когато се е паднало четно число, а \(N\) е общият брой хвърляния.
В тази статия ще използваме класическия подход, тъй като той е по-прост и интуитивно разбираем. Но крайните формули ще бъдат еднакви за двата подхода.
Две събития: обединение и сечение
Нека имаме две събития E и F. Тяхното сечение (\(E \cap F\)) е събитието, когато се случват и двете събития E и F. А обединението (\(E \cup F\)) е събитието, когато се случва поне едно от двете събития E или F.
Например, ако E е “падна се четно число”, а F е “падна се число по-голямо от 3”, то:
$$ E = \{2, 4, 6\} $$$$ F = \{4, 5, 6\} $$$$ E \cup F = \{2, 4, 5, 6\} $$$$ E \cap F = \{4, 6\} $$Графично това е сечението на два кръга на диаграмата на Вен:
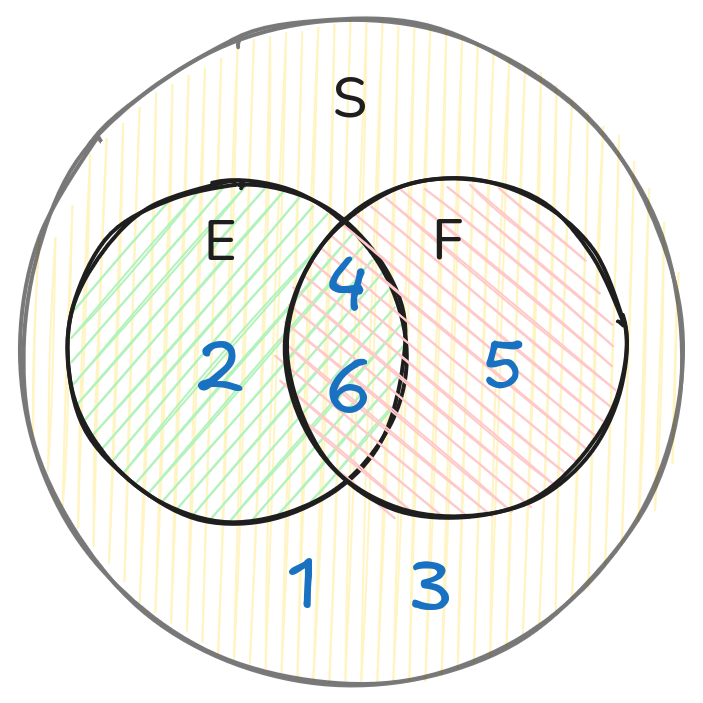
Вероятността, че ще се случи поне едно от двете събития E или F, се обозначава с \(P(E \cup F)\) и се изчислява по формулата:
$$ P(E \cup F) = \frac{|E|}{|S|} + \frac{|F|}{|S|} - \frac{|E \cap F|}{|S|} = \frac{|E \cup F|}{|S|} = P(E) + P(F) - P(E \cap F) \tag{2} $$Тук \(P(E \cup F)\) е вероятността, че ще се случи поне едно от двете събития.
Формулата отчита, че ако събитията E и F се пресичат, то елементите на сечението ще бъдат преброени два пъти, затова изваждаме \(P(E \cap F)\).
Сега да разгледаме вероятността на сечението на две събития:
В нашия пример E е “падна се четно число”, а F е “падна се число по-голямо от 3”. Тогава:
$$ P(E \cap F) = \frac{|E \cap F|}{|S|} = \frac{|\{4, 6\}|}{|S|} = \frac{2}{6} = \frac{1}{3} $$Зависимост и независимост на събитията
Сега да разгледаме зависимостта и независимостта на събитията. Ако събитията E и F са независими, то вероятността на тяхното сечение е равна на произведението на вероятностите на всяко от тях:
$$ P(E \cap F) = \frac{|E \cap F|}{|S|} = \frac{|E|}{|S|} \cdot \frac{|F|}{|S|} = P(E) \cdot P(F) \tag{3} $$За да разберем тази формула интуитивно, нека си представим следното:
Ако \(P(E) = |E|/|S|\) е делът на благоприятните изходи E в пространството S, а \(P(F) = |F|/|S|\) е делът на благоприятните изходи F в пространството S, то ако събитията са независими, то шансът, че в частта на благоприятните изходи E ще има и част от благоприятните изходи F, ще бъде същият като шанса, че във всички изходи S ще има част от благоприятните изходи F.
А ако е така, то тази част от S, която ще бъде в E (\(P(E) \cdot |S|\)), има шанс \(P(F)\) да съдържа благоприятни изходи F. Тоест \(P(E) \cdot P(F) = P(E \cap F)\).
Ако вероятността на събитието E не зависи от това дали е настъпило събитието F, то събитията E и F се наричат независими.
Например, ако хвърляме зар два пъти, то:
$$ S = \{ (1,1), (1,2), \ldots, (6,6) \} $$Нека E е “първото хвърляне е четно”, а F е “второто хвърляне е четно”. Тези събития са независими, тъй като вероятността за четно първо хвърляне не зависи от резултата от второто хвърляне.
За всяко хвърляне половината от изходите са четни:
$$ P(E) = P(F) = \frac{3}{6} = \frac{1}{2} $$Вероятността и двете събития да се случат:
$$ P(E \cap F) = P(E) \cdot P(F) $$В нашия пример след първото от всички възможни изходи благоприятни са точно половината, а след второто хвърляне от тази половина също половината. Тоест:
$$ P(E \cap F) = P(E) \cdot P(F) = \frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4} $$Тази формула е валидна само за независими събития.
Ако вероятността на събитието E зависи от това дали е настъпило събитието F, то събитията E и F се наричат зависими. Обозначава се като \(P(E|F)\) — вероятността на събитието E при условие, че е настъпило събитието F.
Да запомним, че ако събитията E и F са независими, то:
$$P(E|F) = P(E) \tag{4}$$Ако събитията са зависими, то:
$$P(E|F) \neq P(E)$$
За по-добро разбиране нека разгледаме два примера:
Пример 1:
Нека F е “падна се число по-голямо от 3”, а E е “падна се четно число”. Тогава:
$$ P(F) = \frac{3}{6} = \frac{1}{2} $$$$ P(E) = \frac{3}{6} = \frac{1}{2} $$Но
$$ P(E|F) = \frac{|E \cap F|}{|F|} = \frac{|\{4, 6\}|}{|\{4, 5, 6\}|} = \frac{2}{3} $$което не е равно на \(P(E)\).
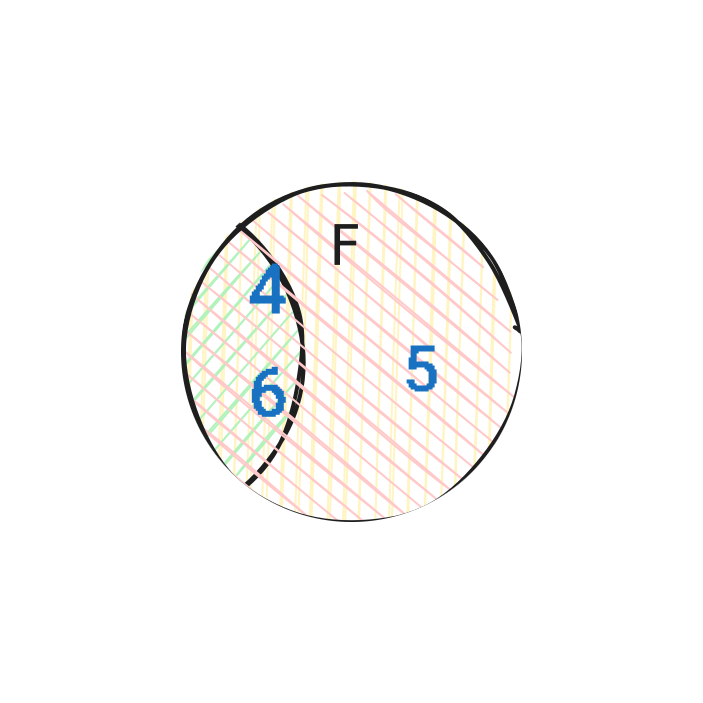
(От 3 четни числа {2, 4, 6} две са по-големи от 3 — {4, 6})
Ако събитията бяха независими, то \(P(E|F) = P(E)\). В случая \(P(E|F) > P(E)\), следователно събитията са зависими.
Пример 2:
Нека E е “падна се едно от числата {1,2,3}”, а F е “падна се едно от числата {1,2,4,6}”.
Ако е настъпило събитието F, то за да настъпи събитието E (падна се едно от {1,2,3}), трябва да се падне 1 или 2. Да проверим това математически:
$$ P(F) = \frac{4}{6} = \frac{2}{3} $$$$ P(E) = \frac{3}{6} = \frac{1}{2} $$Сега ще намерим \(P(E|F)\):
$$ P(E|F) = \frac{|E \cap F|}{|F|} = \frac{2}{4} = \frac{1}{2} $$Обърнете внимание: тъй като знаем, че е настъпило събитието F (паднало се е едно от {1,2,4,6}), разглеждаме само тези числа. В числителя е \(E \cap F\), в знаменателя – броят на елементите в F.
Да сравним \(P(E|F)\) и \(P(E)\): те са равни, следователно събитията са независими.
Ако ни съобщят: “Падна се число от F (тоест 1, 2, 4 или 6)”, това не променя вероятността за попадане в E (без да знаем F: {1,2,3} от {1,2,3,4,5,6}; знаейки F: {1,2} от {1,2,4,6}). Тя остава 3/6 = 2/4 = 0.5. Следователно, информацията за F не помага да разберем дали се е случило E.
Независимостта е информационна слепота:
Знанието за едно събитие не дава информация за другото.
Какво да правим, ако събитията са зависими? На какво е равна вероятността на събитието E при условие, че е настъпило събитието F?
Аналогично на начина, по който обяснихме формулата за сечението на вероятността на независими събития, можем да разсъждаваме и за зависими събития.
Ако събитието F е настъпило, можем да разглеждаме само онези изходи, които съответстват на събитието F. В случай на зависими събития, делът на благоприятните изходи Е, които се пресичат с F, вече не е равен на дела на всички благоприятни изходи E в пространството S.
А ако е така, когато е настъпило F - шансът да се случи и E се е променил! Можем да запишем формула за условната вероятност на събитието E при условие, че е настъпило събитието F:
$$ P(E \cap F) = P(E|F) \cdot P(F) \tag{5} $$От това следва, че:
$$ P(E|F) = \frac{P(E \cap F)}{P(F)} \tag{6} $$Тъй като сечението на две събития E и F е събитието, което е настъпило едновременно, можем аналогично да изразим вероятността P(E∩F) чрез условната вероятност на събитието F при условие, че е настъпило събитието E:
$$ P(E \cap F) = P(F|E) \cdot P(E) \tag{7} $$Като приравним десните страни на (5) и (7), получаваме:
$$ P(E|F) \cdot P(F) = P(F|E) \cdot P(E) $$или
$$ P(E|F) = \frac{P(F|E) \cdot P(E)}{P(F)} \tag{8} $$ТОВА Е ТЕОРЕМАТА НА БЕЙС!
Това е формула, която свързва условните вероятности на две събития E и F. Тя позволява да изчислим вероятността на събитието E при условие, че е настъпило събитието F, знаейки вероятността на събитието F при условие, че е настъпило събитието E.
Често P(F) е неизвестна, но може да бъде изразена чрез пълната вероятност на събитието F:
Формула на пълната вероятност:
$$ P(F) = P(F|E) \cdot P(E) + P(F| \neg E) \cdot P(\neg E) \tag{9} $$където \(\neg E\) е събитието, противоположно на събитието E.
Теоремата на Бейс е формула, която свързва условните вероятности на две събития E и F. Тя позволява да изчислим вероятността на събитието E при условие, че е настъпило събитието F, знаейки вероятността на събитието F при условие, че е настъпило събитието E.
Това е много полезна формула, която позволява да изчисляваме вероятности на събития, когато са известни други вероятности. Тя се използва широко в статистиката, машинното обучение и други области.
Всеки от тези елементи на формулата има своето значение:
- P(E|F) — апостериорна вероятност (това, което искаме да узнаем)
- P(E) — априорна вероятност (първоначално предположение)
- P(F|E) — правдоподобие (likelihood)
- P(F) — пълна вероятност на събитието F
Детайлното разглеждане на всеки от тези елементи излиза извън обхвата на тази статия, но като цяло можем да кажем, че:
- A priori (априорна) вероятност — това е вероятността на събитието преди получаването на нова информация.
- A posteriori (апостериорна) вероятност — това е вероятността на събитието след получаването на нова информация.
- Правдоподобие (likelihood) — това е вероятността да наблюдаваме данните, ако хипотезата е вярна.
- Пълна вероятност (marginal likelihood) — това е вероятността да наблюдаваме данните, независимо от хипотезата.
Всяка от тези вероятности има своето значение и се използва като основа за алгоритми на статистиката и машинното обучение, като байесови мрежи, наивен байесов класификатор, MLE, ELBO, MCMC и много други.
Дядо Иван, условна вероятност и теоремата на Бейс
Няколко примера
Да разгледаме пример.
Дядо Иван попадна на бирен фестивал. Организаторите устроиха томбола: от 50 бутилки (40 светли, от които 9 безалкохолни, и 10 тъмни, от които 3 безалкохолни).

Пример 1:
Нека започнем с прост въпрос: “Каква е вероятността бутилката да е безалкохолна?” Отговорът е прост: 12/50 = 0.24.
Но какво ако знаем, че бутилката е тъмна? Каква е вероятността тя да е безалкохолна?
В този случай разглеждаме само тъмните бутилки. От 10 тъмни бутилки 3 са безалкохолни, следователно вероятността е 3/10 = 0.3.
Сега с помощта на формулата на Бейс можем да изразим вероятността бутилката да е тъмна, при условие че е безалкохолна:
$$ P(\text{тъмна} | \text{безалкохолна}) = \frac{P(\text{безалкохолна} | \text{тъмна}) \cdot P(\text{тъмна})}{P(\text{безалкохолна})} = \frac{3/10 \cdot 10/50}{12/50} = \frac{3}{12} = 0.25 $$Това съвпада с интуитивното разбиране: от 12 безалкохолни бутилки 3 са тъмни, следователно вероятността безалкохолната бутилка да е тъмна е 0.25.
Пример 2:
Дядо Иван и приятелят му Петър се състезават кой по-добре определя бирата.
- И двамата независимо опитват една и съща бутилка. Дядо Иван правилно определя типа бира с вероятност 0.7, а Петър – с вероятност 0.65. Каква е вероятността поне един от тях да определи правилно типа на случайно избраната бира?
Решение:
$$ \begin{aligned} P(\text{поне един}) &= 1 - P(\text{и двамата сгрешиха}) \\ &= 1 - P(\text{грешка дядо Иван}) \cdot P(\text{грешка Петър}) \\ &= 1 - (1 - 0.7) \cdot (1 - 0.65) \\ &= 1 - 0.3 \cdot 0.35 \\ &= 1 - 0.105 = 0.895 \end{aligned} $$- Дядо Иван със завързани очи опита бирата и каза, че е тъмна алкохолна. Известно е, че той правилно определя светлата алкохолна с вероятност 0.7, светлата безалкохолна с вероятност 0.6, тъмната алкохолна с вероятност 0.8 и тъмната безалкохолна с вероятност 0.7. Ако дядо Иван заяви, че бирата е светла, каква е вероятността тя да е алкохолна?
Решение:
Брой бутилки от различни типове:
- Светла алкохолна: 40 - 9 = 31 бутилки
- Светла безалкохолна: 9 бутилки
- Тъмна алкохолна: 10 - 3 = 7 бутилки
- Тъмна безалкохолна: 3 бутилки
Вероятности за различните типове бира:
$$P(\text{светла алкохолна}) = \frac{31}{50} = 0.62$$Да определим вероятностите за определяне на “светла” за всеки тип бира:
- Ако бирата е светла алкохолна: $$P(\text{ще каже "светла"} | \text{светла алкохолна}) = 0.7$$
- Ако бирата е светла безалкохолна: $$P(\text{ще каже "светла"} | \text{светла безалкохолна}) = 0.6$$
- Ако бирата е тъмна алкохолна: $$P(\text{ще каже "светла"} | \text{тъмна алкохолна}) = 1 - 0.8 = 0.2$$
- Ако бирата е тъмна безалкохолна: $$P(\text{ще каже "светла"} | \text{тъмна безалкохолна}) = 1 - 0.7 = 0.3$$
По формулата на пълната вероятност:
$$ \begin{aligned} P(\text{ще каже "светла"}) &= \sum_i P(\text{ще каже "светла"} | \text{тип}_i) \cdot P(\text{тип}_i) \\ &= 0.7 \cdot 0.62 + 0.6 \cdot 0.18 + 0.2 \cdot 0.14 + 0.3 \cdot 0.06 \\ &= 0.434 + 0.108 + 0.028 + 0.018 = 0.588 \end{aligned} $$Нека намерим вероятността за алкохолна бира:
Сега използваме формулата на Бейс (8). Първо ще намерим вероятността дядо Иван да каже “светла” при условие, че бирата е алкохолна:
$$ \begin{aligned} P(\text{ще каже "светла"} | \text{алкохолна}) &= \frac{P(\text{ще каже "светла"} | \text{светла алк}) \cdot P(\text{светла алк})}{P(\text{алкохолна})} \\ &+ \frac{P(\text{ще каже "светла"} | \text{тъмна алк}) \cdot P(\text{тъмна алк})}{P(\text{алкохолна})} \\ &= \frac{0.7 \cdot 0.62 + 0.2 \cdot 0.14}{0.76} \\ &= \frac{0.434 + 0.028}{0.76} \\ &= \frac{0.462}{0.76} = 0.6079 \end{aligned} $$Накрая прилагаме формулата на Бейс:
$$ \begin{aligned} P(\text{алкохолна} | \text{ще каже "светла"}) &= \frac{P(\text{ще каже "светла"} | \text{алкохолна}) \cdot P(\text{алкохолна})}{P(\text{ще каже "светла"})} \\ &= \frac{0.6079 \cdot 0.76}{0.588} \\ &= \frac{0.462}{0.588} \approx 0.7857 \end{aligned} $$Следователно вероятността бирата да е алкохолна, при условие че дядо Иван е казал “светла”, е 0.7857.
Заключение
В тази статия разгледахме основите на вероятността, условната вероятност и теоремата на Бейс. Те са важни концепции в статистиката и машинното обучение, които ни помагат да разберем как да работим с вероятности и как да правим изводи на базата на наличната информация.